Notes on Synthesis
A somewhat random collection of personal exploration on synthesis.
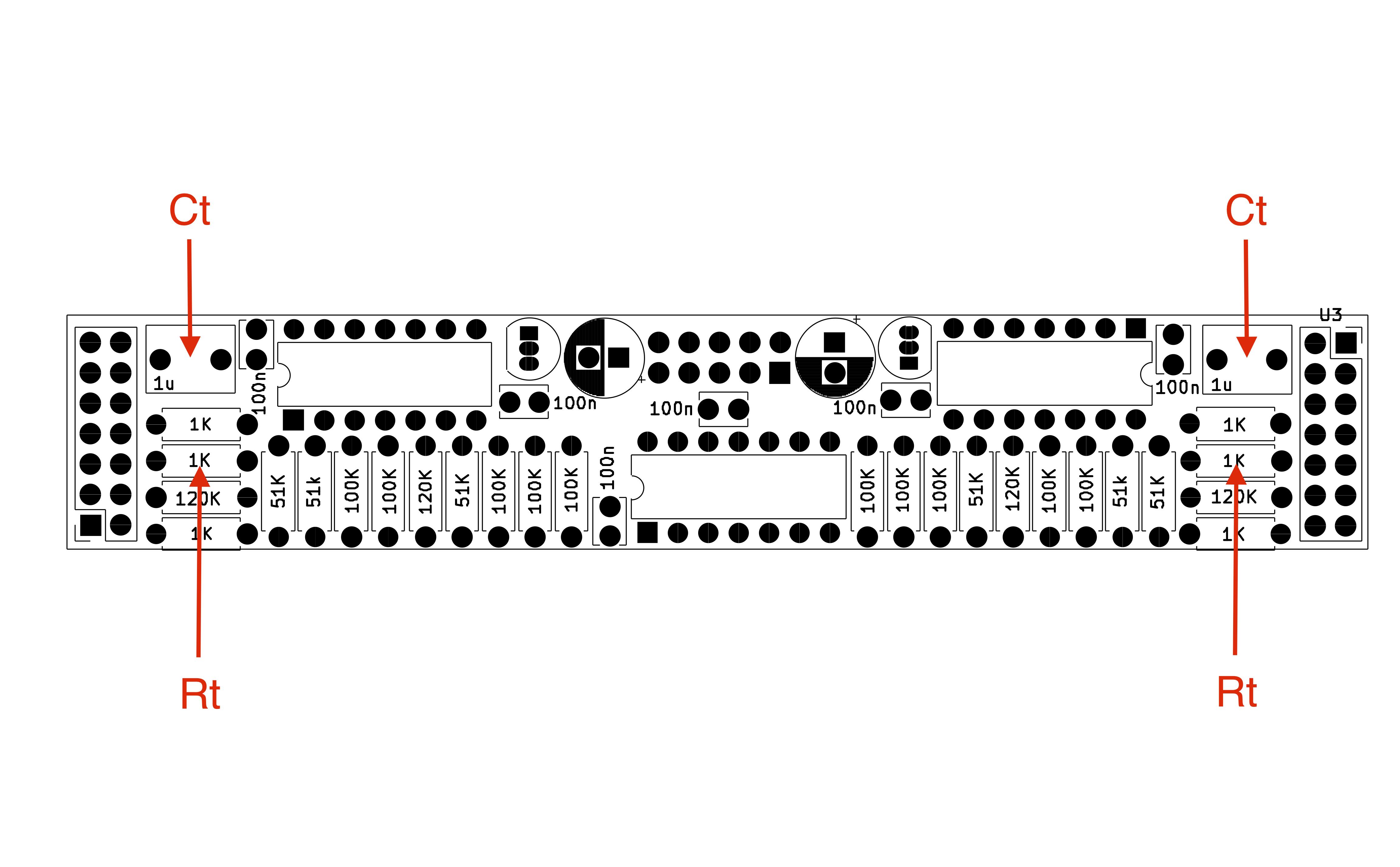
Controlling MRG LFOs frequency range
The MRG LFOs contains two different oscillator cores, each capable of oscillating from slightly more than a second to about 600Hz.
read moreWith apologies to Paganini
This is what happens when you feed a MIDI file of Paganini’s Capriccio no. 24 to a monosynth built with MRG modules :
read moreThe Yamaha DX7 Envelope Generator, part four.
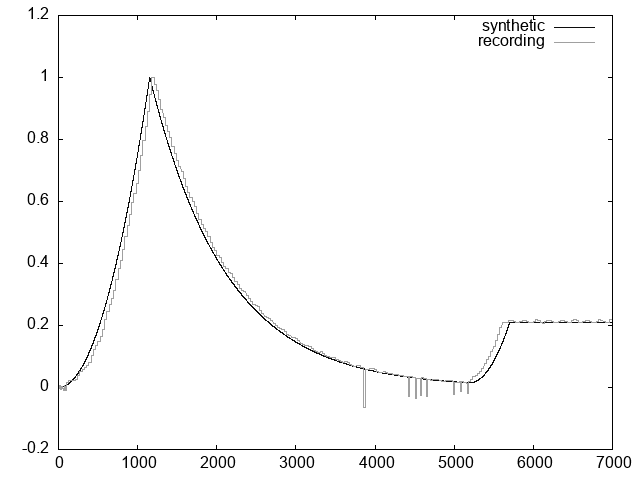
This is part four of a qualitative analysis of the DX7 Envelope Generator. The series begins here .
Part three is here Rising segments.
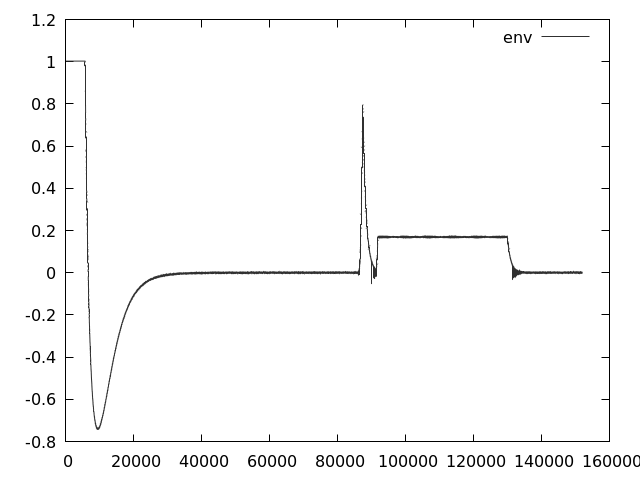
read moreThe Yamaha DX7 Envelope Generator, part three.
Part two is here Extracting the envelope. We concluded part two finding out that the DX7 envelope generator’s curves were:
read moreThe Yamaha DX7 Envelope Generator, part two.
Part one is here A closer look at an operator envelope. Let’s begin our understanding of the envelope generators by trying to answer the easier question: what kind of shape the envelope segments have.
read moreThe Yamaha DX7 Envelope Generator, part one.
Silence, sine waves and trigonometry. The Yamaha DX7, an FM synthesizer released in 1983, should need little or no introduction.
read more